


Next: Multiple classes
Up: 7 Numerical problems and
Previous: 7 Numerical problems and
Contents
Numerical methods are a collection of techniques for solving
mathematical problems which lend themselves to implementation as
computer programs. They exist to solve all sorts of problems, for
example differentiation, minimisation, sorting data and solving
differential equations. Numerical methods are particularly useful
when it is either impossible or impractical to solve a problem
analytically.
The trapezium rule for numerical integration of a function f (x) is
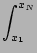 f
f (
x)
dx =
h[
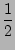 f1
f1 +
f2 +
f3 + ... +
fN-1 +
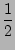 fN
fN] +
O(
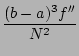
)
=
h[
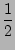
(
f1 +
fN) +
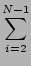 fi
fi]
Here you will use the trapezium rule to numerically integrate a
function. This exercise will allow you to put into practice many
aspects of Java programming that you have learnt so far. A
reminder/primer on the trapezium rule can be found in
Appendix C.
Exercise 7.1
(20 marks)
Write a program that will make use of the trapezium rule to
numerically integrate a mathematical function.
The following steps are given as a guide on how to proceed with the
program. It is recommended that you follow these steps closely to get
all the available marks.
- Write a separate method to return the value of the function
you want to integrate. For example, this is a definition of
f (x) = 2x:
public static double f(double x)
{
return 2*x;
}
- Write a method which implements the trapezium rule. It
should take as arguments the range over which to integrate (x1
and xN) and the number of steps (N). It should use these
parameters to compute the integration using the trapezium rule and
return the result. It will call the method f you defined
in the previous step.
- Write a main method to prompt the user to type in
values of x1, xN, and N, call the above method and print
the result. It should check the value of N supplied is valid
before proceeding to any calculation, but it is sufficient just to
exit with a auitable error message if the value is invalid.
- Test your program, using a function linear in x as shown above,
first with N = 1 (which should fail the
validity check) then N = 2 and a few values where N > 2. Calculate
the answer by integrating the function by hand. You should get
exactly the right answer regardless of the value of N (why?)
- Next, test your program with a second order polynomial for
several values of N. Again, compare with the analytical (hand
calculated) result.
- Study what happens to the accuracy of the answer as N increases.
Show how the convergence relates to N. Is this what you expect
from the formula for the trapezium rule?
- Based on your findings, devise a method to estimate the accuracy of
a calculation when the correct answer is unknown.
At this point you should have established enough confidence in your
program to use it on a function which cannot be integrated
analytically.
When you have written your program, show a demonstrator that it
works. You will then be allocated a function to integrate from those
below. It will help to sketch the function before you try to integrate
it.
- (i)
- The function
x4log(x +
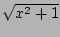 ) over the interval x = 0, 1.
) over the interval x = 0, 1.
- (ii)
- The function
log(3x2) over the interval x = 0.7, 2.
- (iii)
- The function cos(x2) over the interval x = - 1, 1.
- (iv)
- The function cos(x3) over the interval x = - 1, 1.
- (v)
- The function sin(x2) over the interval x = 0, 1.7.
- (vi)
- The function sin(x3) over the interval x = 0, 1.4.
- (vii)
- The function
-log(sin(x)) over the interval x = 0.1, 1.
- (viii)
- The function
cos(tan(x)) over the interval x = - 1, 1.
Make sure you document the design, code and
testing of your program as well as the final result. Most of
the marks for this exercise will be awarded for these three things. As
well as giving the answer, estimate the accuracy of this number using
the method you devised in step 7 above. An accuracy of around 3
significant figures is sufficient.



Next: Multiple classes
Up: 7 Numerical problems and
Previous: 7 Numerical problems and
Contents
RHUL Dept. of Physics
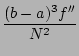 )
)
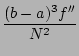 )
)