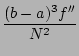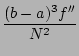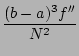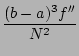


Next: Programming
Up: C. Trapezium rule for
Previous: Trapezium rule
Contents
To make this rule useful, break the curve to be integrated into many
small intervals (small h). Then use the trapezium rule many times,
like this (see figure C.5):
Figure C.5:
The curve f (x) is now approximated by a series of short
straight lines which each form a trapezium. Summing the area of
these trapezia gives an approximation of the total area under the
curve between a and b.
|
|
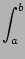 f (x)dx f (x)dx |
= |
h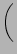 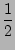 f1 + f1 + 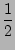 f2 f2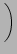 ..A ..A |
|
| |
|
+ h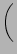 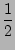 f2 + f2 + 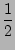 f3 f3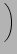 ..B ..B |
|
| |
|
+ h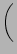 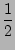 f3 + f3 + 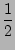 f4 f4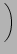 ..C ..C |
|
| |
|
+ h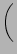 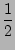 f4 + f4 + 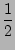 f5 f5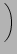 ..D ..D |
|
| |
|
+ O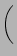 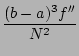 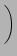 |
|
Generalise the formula to N points:
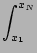 f
f (
x)
dx =
h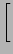
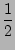 f1
f1 +
f2 +
f3 + ... +
fN-1 +
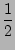 fN
fN![$\displaystyle \left.\vphantom{
\frac{1}{2}f_1 + f_2 + f_3 + ... + f_{N-1} + \frac{1}{2}f_N }\right]$](img33.png)
+
O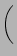
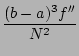
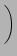
Note that h is still the width of a single interval, so
h =
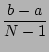
The approximation error is now
b - a and f'' are normally fixed parameters of the problem.
You can see that increasing N will improve the accuracy.



Next: Programming
Up: C. Trapezium rule for
Previous: Trapezium rule
Contents
RHUL Dept. of Physics
![\includegraphics[width=8cm]{trapint2}](img22.png)
![\includegraphics[width=8cm]{trapint2}](img22.png)