PH291 Stellar Astrophysics Problem Sheet 2

Question 1

Here is a table of the properties of some nearby stars, plus the sun for reference.

Name Type AbsMagnitude M/M_sun R/R_sun

Rigel B8 Ia -6.69 10 28

Sirius A A1 V +1.45 2.2 1.6

The Sun G2 V +4.83 1 1

Proxima Centauri M4 V +15.45 0.1 0.145

R_sun = 7 x 10⁸ m, M_sun = 2 x 10³⁰ kg, L_sun = 3.9 x 10²⁶ W. In the Stefan-Boltzmann law the constant s = 5.67 x 10^-8

1) Calculate the luminosity of each star, in units L_sun.

To calculate L we need to use M₁ - M₂ = -2.5 log₁₀ (L₁/L₂ ) see table below.

L_star = 10^{-0.4(Mstar - Msun)} L_sun

2) Calculate the dynamical, thermal and nuclear timescales for each star (other than the sun-we did that in lectures). Comment on what we might expect for the relative lifetimes of the different stars.

Tdyn = (R³/2GM)^1/2

Tthermal = GM²/RL

Tnuclear= 10^-3 Mc²/L

We can see that the large stars have longer dynamical timescales- makes sense, they are physically bigger so any sort of disturbance is going to take longer to cross the star than it would a small star. But their thermal and nuclear timescales are very much shorter than they are for smaller stars. So while Proxima Centauri might have a lifetime of billions of years, Rigel is only going to live of order of a hundred million years or so at most.

3) Consider a simple model star where nuclear burning takes place in the region m=0 to m=0.4 M_star. The rate of nuclear energy release in that region is a constant, q₀, and outside that region is zero. Assumng everything is in thermal equilibrium, calculate an expression for how the energy crossing the surface at m, F(m), varies from m=0 to m=M_star.

We need to use dF/dm = q

remember q is a function of m!

For m=0 to m=0.4 M_star, q(m) = q₀ and for m=0.4 M_star to m=M_star q(m) = 0

so Integrate dF/dm = q and we get

F(m) = q₀ m + c1 (0 < m < 0.4 M_star) and

F(m) = c2 (0.4 M_star < m < M_star )

we can fix the values of the constant of integration c1 by noting that F(0) = 0 (no nuclear burning if there is no mass contained in the shell) and of c2 by noting that the function F(m) must be continuous so the value of c2 is the value of F(0.4 M_star).

Question 2

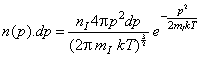
1) The distribution of momenta of particles in a classical ideal gas in thermodynamic equilibrium is given by the Maxwell distribution:

Plot a graph of this function for Hydrogen ions (m_I = 1.66 x 10^-27 kg) in the core of the sun, at T= 10⁷ K, taking the normalisation factor n_I = 1. Plot the function for values of particle speed from 0 to 10⁶ m/s (and remember p = mv).

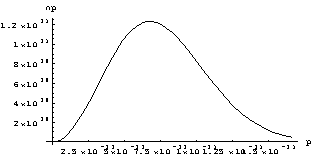
Here is a graph from Mathematica:

To plot it without the help of Mathematica, just notice that the distribution proportionally to p², and so is zero for p=0, and decreases as e^-p.p, so there must be a maximum at some point. Get that point by setting the derivative wrt p to zero. Replacing p by mv, it turns out the mode of the distribution is around v=3 x 10⁵ m/s.

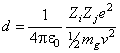
2) Classically, nuclear fusion can only take place if the kinetic energy of the ion is enough to overcome the Coulomb barrier. From lectures, the distance of closest approach of a classical particle to another one is given by:

Calculate the distance of closest approach for two Hydrogen nuclei (Z=1, m_g = 1.66 x 10^-27 kg) and a velocity of 3 x 10⁵ m/s (which is typical of particles in the core of the sun). What velocity would the nucleus have to have to have in order to get within a distance of d=10^-15 m of the other one? This distance is characterstic of strong nuclear processes and would be close enough to allow the two nuclei to fuse.

Simply substitute the value of v=3 x 10⁵ m/s in the expression. This gives the distance of closest approach between the two Hydrogen nuclei at thermal velocity typical of the solar core as 3.1 x 10^-12 m. This is something like 3000 times larger than the approximate size of a small nucleus (~10^-15m).

Now we just have to solve for v when d=10^-15 m. This gives a velocity of at least 1.7 x 10⁷ m/s. That’s a good factor of 50 or so more than the most probable speed we found from the graph in part a).

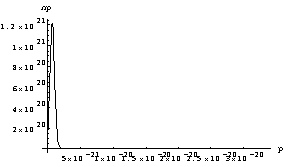3) Replot the graph you did in part a) over a range including the velocity you calculated in part c). Comment on the chances of fusion happening in the classical case.

Using Mathematica again to plot from v=0 to v= 2 x 10⁷ m/s:

The probability of finding a particle with velocities of the order of 10⁷m/s becomes too small to see on a plot. We can however note that in the exponential we have exp(-p²/2 m_I k T), which if we put in the constants we can re-express as exp(-(mi v)²/ 2 m_I k T) = exp(-v² x 6.0 x 10^-12).

If we put in v = 3 x 10⁵ m/s we get exp(-0.54) = 0.58 which is quite respectable.

If we put in v = 1.7 x 10⁷ m/s we get exp(-1740) = something much too small for my calculator.

We can conclude that the classical probability of fusion in the solar core is vanishingly small.

4) We saw in the lecture on composition that the rate of nuclear burning rises with temperature. The virial theorem shows that a star which behaves like an ideal gas has a negative heat capacity. What would happen to a theoretical star that had a positive rather than negative heat capacity?

The rate of nuclear burning would increase, leading to a rise in temperature and eventually a nuclear thermal runaway.

5) Starting from the Maxwell distribution quoted above, and using the pressure integral as given in lectures, show that the equation of state for a classical ideal gas is P=nkT.

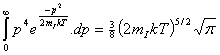
Note that

If everything is in thermal equilibrium, calculate an expression for how the energy crossing the surface at m, i.e. F(m), varies from m=0 to m=M_star.

Starting from the pressure integral:

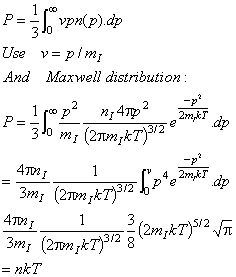
If everything is in thermal equilibrium, we have dF/dm = q…