


Next: Extended trapezium rule
Up: C. Trapezium rule for
Previous: C. Trapezium rule for
Contents
The trapezium rule states that you can approximate the area under a
curve by a trapezium, as shown in figure C.4. The area is
therefore calculated like this:
Figure C.4:
A straight line is used to approximate the curve f (x)
between x1 and x2. This forms a trapezium (shaded area) which can be
used to calculate approximately the area under
the curve between these bounds.
|
|
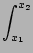 f
f (
x)
dx =
h
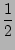 f1
f1 +
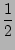 f2
f2
+
O(
h3f'')
Where the notation f1 is short hand for f (x1).
The error due to the approximation,
O(h3f''), indicates that this
method is exact for polynomials up to degree 1, i.e. straight lines
f (x) = ax + b, because for such functions the second derivative
f'' = 0. It is clearly an approximation for higher order polynomials
(x2,x3, etc.) and other functions. The error will also be small
if h is small.
The area of a trapezium is its average height x its width, i.e.
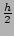 (f1 + f2).
(f1 + f2).



Next: Extended trapezium rule
Up: C. Trapezium rule for
Previous: C. Trapezium rule for
Contents
RHUL Dept. of Physics
![\includegraphics[width=8cm]{trapint1}](img17.png)
![\includegraphics[width=8cm]{trapint1}](img17.png)
![]() (f1 + f2).
(f1 + f2).